1. 시간 복잡도(Time complexity)란?
알고리즘의 성능을 나타내는 지표로, 입력 크기에 대한 연산 횟수의 상한을 의미한다.
입력 크기 : 알고리즘이 처리해야 할 데이터의 양
코딩 테스트 기준으로 대략적으로 기억하자. "컴퓨터가 초당 연산할 수 있는 최대 횟수는 1,000~2,000만 번이다."

2. 점근적 표기법
O(N), O(1), O(NlogN) 처럼 입력 크기에 따른 연산 횟수의 "추이"를 활용해서 시간 복잡도를 표현하는 방법을 점근적 표기법이라고 한다.
가장 많이 사용하는 점근적 표기법은 상한선을 활용하는,
즉 최악의 경우의 시간 복잡도를 표현하는 빅오 표기법(big-O notation)이다.
3. 파이썬은 부동소수형 데이터를 다룰 때 오차가 발생한다.
파이썬은 부동소수형 데이터를 이진법으로 표현하기 때문에, 표현 과정에서 엡실론(epsilon)이라고 하는 오차가 발생한다.
EX) 0.1을 3번 더한 a의 값에 0.3을 빼면 0이 아니다.
4. 문자열 수정
문자열(string)은 immutable 객체이므로, 문자열을 수정하고 싶다면, 문자열.replace() 메서드를 사용하면 된다.

5. 코딩 테스트 구현 노하우 - 보호 구문 (guard clauses)
보호 구문은 본격적인 로직을 진행하기 전, 예외 처리 코드를 추가하는 기법이다.
5-2. 합성 함수 (Composite method)
2개 이상의 함수를 활용하여, 함수를 추가로 만드는 기법이다. 보통 합성 함수는 람다식을 활용한다.

6. 배열 연산의 시간 복잡도
배열은 임의 접근(random access)이라는 방법으로 배열의 모든 위치에 있는 데이터를 단 한 번에 접근할 수 있다.
데이터에 접근하기 위한 시간 복잡도 : O(1)
배열 맨 뒤에 데이터를 추가할 경우 : O(1)
배열 맨 앞에 데이터를 추가할 경우 : O(N)
배열 중간에 데이터를 추가할 경우 : O(N)
6-2. 배열을 선택할 때 고려할 점
1) 할당할 수 있는 메모리 크기를 확인해야 한다.
보통 정수형 1차원 배열은 1000만 개, 2차원 배열은 3000 * 3000 크기를 최대로 생각한다.
2) 중간에 데이터 삽입이 많은지 확인해야 한다.
7.자주 사용하는 리스트 기법
1) insert() 메서드로 데이터 삽입 -> insert() 메서드는 특정 위치에 데이터를 삽입할 수 있다.

2) pop() 메서드는 pop할 데이터의 "인덱스"를 인수로 받아 삭제하고, 삭제한 데이터의 값을 반환한다.

3) remove() 메서드는 pop()과는 다르게, 특정 "데이터 자체"를 삭제하는 함수이다.
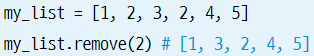
이 상태에서 remove(2)를 실행하면 첫 번째 위치에 있는 2를 삭제한다.
4) index() 메서드는 특정 데이터가 처음 등장한 인덱스를 반환한다. 없으면 -1를 반환한다.
8. 해시 (Hash)
해시는 해시 함수를 사용해서 변환한 값을 인덱스(해시값)로 삼아,
키와 값을 저장해서 빠른 데이터 탐색을 제공하는 자료구조이다.
해시는 키와 데이터를 일대일 대응하여 저장하므로, 키를 통해 데이터에 바로 접근할 수 있다. (데이터 탐색이 빠르다)
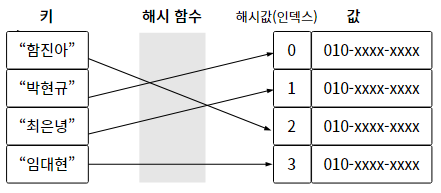
8-1. 해시의 특징
1) 해시는 단방향으로 동작한다. 즉, 키를 통해 값을 찾을 수 있지만, 값을 통해 키를 찾을 수는 없다.
※ 단방향으로 동작하는 해시의 특성은 외부에 정보를 안전하게 제공한다는 특징도 되므로 -> 네트워크 보안에서 많이 활용된다.
2) 찾고자 하는 값을 O(1)에서 바로 찾을 수 있다.
-> 키 자체가 해시 함수에 의해 값이 있는 인덱스가 되므로 값을 찾기 위한 탐색 과정이 필요 없다.
3) 값을 인덱스로 활용하려면, 적절한 변환 과정을 거쳐야 한다.
해시 테이블 (Hash table) : 키와 대응한 값이 저장되어 있는 공간
버킷 (bucket) : 해시 테이블의 각 데이터
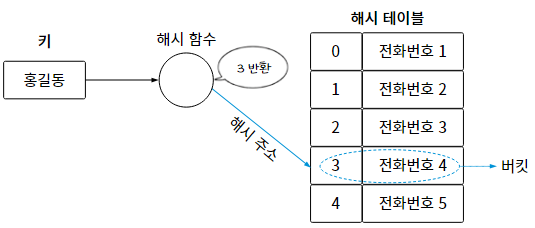
8-2. 해시의 특성을 활용하는 분야
1) 비밀번호 관리 : 해시 함수를 활용해 해싱(Hashing)한 비밀번호를 데이터베이스에 저장한다.
비밀번호가 맞는지 확인할 때도 마찬가지로, 사용자가 입력한 비밀번호를 해싱해서 확인한다.
2) 데이터베이스 인덱싱 : 데이터베이스에 저장된 데이터를 효율적으로 검색할 때, 해시를 활용한다.
3) 블록체인 : 블록체인에서 해시 함수는 핵심 역할을 한다.
각 블록은 이전 블록의 해시값을 포함하고 있으며, 이를 통해 데이터 무결성을 확인할 수 있다.
9. 해시 함수
9-1. 해시 함수를 구현할 때 고려해야 할 내용
1) 해시 함수가 변환한 값은 인덱스로 활용해야 하므로, 해시 테이블의 크기를 넘으면 안된다!
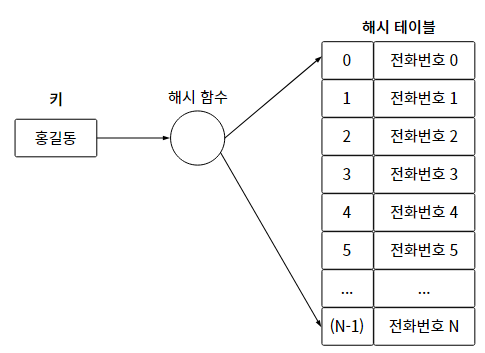
2) 해시 함수가 변환한 값의 충돌은 최대한 적게 발생해야 한다.
충돌 : 서로 다른 두 키에 대해 -> 해시 함수를 적용한 결과가 동일한 것
※ 충돌이 아예 발생하지 않는 해시 함수는 거의 없다!
9-2. 자주 사용하는 해시 함수
1. 나눗셈법 (division method)
키를 "소수"로 나눈 나머지를 활용한다. 그러면 소수가 아닌 값 N으로 나누면 안될까?
N의 약수 중 하나를 M이라고 한다면, 임의의 수 O에 대해 M * O = N이 되는 수가 반드시 있다.
EX) N = 15이고, M = 3인 경우에 O = 5가 된다. 그러면 O를 주기로 같은 해시값이 반복된다!
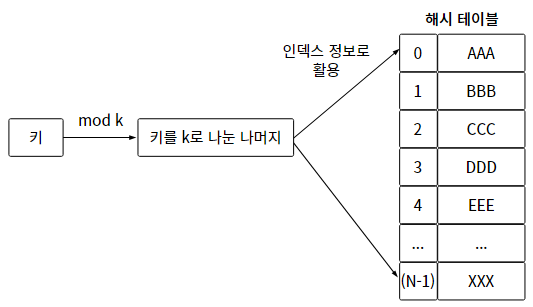
나눗셈법의 해시 테이블의 크기는 k이다. -> k에 대해 모듈러 연산을 했을 때, 나올 수 있는 값은 0 ~ (k-1)이기 때문이다.
즉, 나눗셈법은 아주 많은 데이터를 저장해야 하는 상황이라면 굉장히 큰 소수가 필요하고,
이때 매우 큰 소수는 기계적인 방법으로 구해야 한다는 단점이 있다.
2. 곱셈법 (multiplication method)
나눗셈법과 비슷하게 모듈러 연산을 활용하지만 소수는 활용하지 않는다는 장점이 있다.
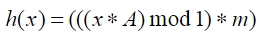
m은 최대 버킷의 개수, A는 황금비(golden ratio number, 대략 1.618033.. 또는 소수부 0.6183만 사용)이다.
다음과 같은 공식에 적용하면 데이터를 테이블의 인덱스 범위인 0 ~ (m - 1)에 매치할 수 있다.
3. 문자열 해싱
키의 자료열이 문자열일 때도 사용할 수 있는 해시 함수이다.
문자열의 문자를 숫자로 변환하고, 이 숫자들을 다항식의 값으로 변환해서 해싱한다.

이 공식에서 p는 31 (홀수, 메르센 소수)이고, m은 해시 테이블의 최대 크기이다.
메르센 소수 : 2^N - 1 형식으로 표시할 수 있는 숫자 중에서 소수인 수.
해시에서 충돌을 줄이는데 효과적이라는 연구결과가 있다.

그런데, 이런 "apple"이라는 간단한 문자열을 해싱했는데도 결과값은 4,990,970으로 굉장히 크다.
오버플로우가 발생할 여지가 있으므로 아래 연산 법칙을 활용해 문자열 해시 함수를 수정할 수 있다.

해시 함수뿐 아니라, 보통 수식에 모듈러 연산이 있는 문제 중 큰 수를 다루는 문제는 이런 오버플로우 함정이 있기도 하다!
난이도가 높은 문제는 대부분 이런 함정을 포함하고 있으니, 주의해야 한다.
10. 충돌 처리
10-1. 체이닝(chaining)으로 처리하기
체이닝은 충돌이 발생하면, 해당 버킷에 연결 리스트(linked list)로 같은 해시값을 가지는 데이터를 연결하는 간단한 방법이다.
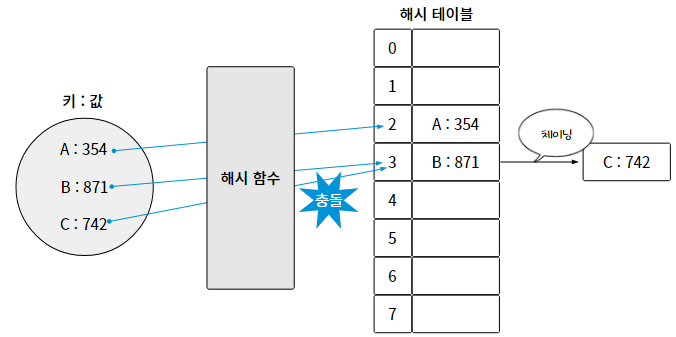
체이닝의 2가지 단점
1) 해시 테이블 공간 활용성이 떨어짐
충돌이 많아지면 그만큼 연결 리스트의 길이는 길어지고, 다른 해시 테이블의 공간은 덜 사용하기 때문에
2) 검색 성능이 떨어짐
연결 리스트 자체의 한계 때문에 검색 성능이 떨어진다. 연결 리스트는 항상 값을 찾을 때, 맨 앞 데이터부터 검색해야 하기 때문에
10-2. 개방 주소법(open addressing)으로 처리하기
빈 버킷을 찾아 충돌값을 삽입하는 방식으로,
해시 테이블을 최대한 활용하므로 체이닝보다 메모리를 더 효율적으로 사용한다는 장점이 있다.
1) 선형 탐사 방식 (linear probing)
충돌이 발생하면, 다른 빈 버킷을 찾을 때까지 일정한 간격(보통 1)으로 이동한다. m은 수용할 수 있는 최대 버킷이다.


그러나 충돌 발생시 1칸씩 이동하며 해시 테이블 빈 곳에 값을 넣으면, 해시 충돌이 발생한 값끼리 모이는 영역이 생긴다.
이를 클러스터(cluster)가 형성된다고 하는데, 이런 군집이 생기면 해시값은 겹칠 확률이 더 올라간다.
※ 그래서 이를 방지하기 위해, 제곱수만큼 이동하며 탐사하는 방법도 있다!
2) 이중 해싱 방식
말 그대로 해시 함수를 2개 사용하거나, 때에 따라 N개로 늘리는 방식이다.
두 번째 해시 함수의 역할은 첫 번째 해시 함수로 충돌이 발생하면, 해당 위치를 기준으로 어떻게 위치를 정할지 결정하는 역할을 한다.
EX) h1이 1차 해시 함수, h2가 2차 해시 함수라고 하자.
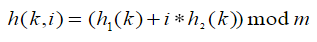
수식을 보면, 선형 탐사와 비슷하게 더하는 방식으로 데이터의 위치를 정하지만, 클러스터를 줄이기 위해 m을 제곱수로 하거나 소수로 한다.
해시 함수 자체를 구현하라는 문제는 나오지 않을 가능성이 높지만, 이 개념 자체는 중요하고 볼 수 있다!
11. 트리 (Tree)
트리는 데이터를 저장하고 탐색하기에 유용한 자료구조이다.
11-1. 트리의 특성을 활용하는 분야 3가지
프로그래밍 분야에서 트리는 "계층 구조"를 표현하는 용도로 많이 사용한다.
EX) 파일 시스템이나 디렉터리 구조 등을 트리로 구성하거나 관리할 수 있다.
1) 기계학습 : 기계학습의 한 종류 중 의사 결정 트리(Decision Tree)가 있다.
이를 통해 외부에서 입력된 데이터를 분류하거나 상황을 예측하는 모델을 만들 수 있다.
2) 자동 완성 기능 : 트리는 문자열 처리에도 많이 활용된다. 검색 엔진에서 검색어 추천 기능도 트라이(trie)라는 독특한 트리 구조를 활용한 것이다. 이를 활용하면, 접두사나 패턴 검색을 쉽게 할 수 있다.
3) 데이터베이스 : 데이터를 쉽게 검색, 삽입, 삭제할 수 있도록 트리를 활용해서 데이터를 구조화하고 인덱싱한다.
이때, B-트리나 B+트리를 많이 사용한다.
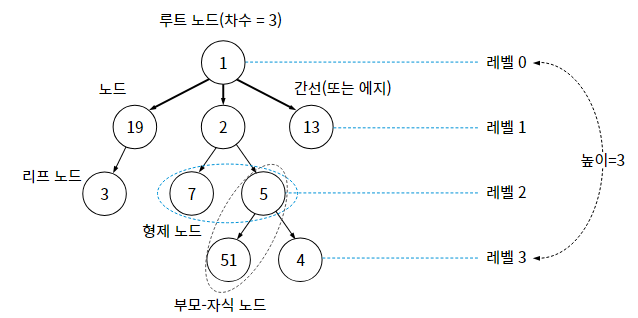
※ 코딩 테스트에서는 이진 트리 (binary tree)만 제대로 알고 있으면 충분하다. (모든 노드의 degree가 2이하인 트리)
12. 이진 트리를 배열이나 포인터로 표현하기
배열은 선형 자료구조이고, 트리는 계층 자료구조이다. 따라서 배열을 트리를 표현하려면 아래 3가지 규칙이 필요하다.
참고로 이 규칙은 루트 노드를 배열 인덱스 1번이라고 생각하여 작성한 규칙이다.
1) 루트 노드는 배열 인덱스 1번에 저장한다.
2) 왼쪽 자식 노드의 배열 인덱스는 "부모 노드의 배열 인덱스 x 2" 이다.
3) 오른쪽 자식 노드의 배열 인덱스는 "부모 노드의 배열 인덱스 x 2 + 1" 이다.
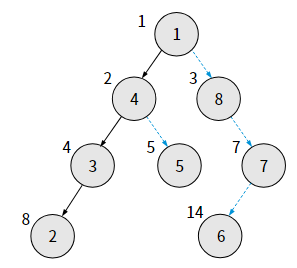

반대로 루트 노드의 인덱스를 0번으로 하면,
2) 왼쪽 자식 노드의 배열 인덱스는 "부모 노드의 배열 인덱스 x 2 + 1" 이다.
3) 오른쪽 자식 노드의 배열 인덱스는 "부모 노드의 배열 인덱스 x 2 + 2" 이다.
이진 트리를 배열로 표현하면 -> 자식이 없거나 쓰지 않는 인덱스들은 모두 빈 값이므로 메모리가 낭비된다는 단점이 있다.
그렇다고 해서 배열 표현 방법이 나쁘다는 것은 아니다.
이진 트리를 배열로 표현하는 방식은 굉장히 구현 난이도가 쉬우므로, 메모리만 넉넉하다면 구현 시간을 단축할 수 있다.
또한 대부분의 코딩 테스트에서는 배열로 이진 트리를 구현해도 괜찮은 경우가 많다.
※ 이진 트리의 노드가 N개일 때, 배열로 이진 트리를 생성하면 O(N)의 시간이 소요된다.
12-1. 이진 트리 3가지 순회 방법
방문 : 탐색을 마친 상태를 말한다. 탐색 과정에서 "노드를 지나치는 것"과 "노드를 방문하는 것"은 다르다.
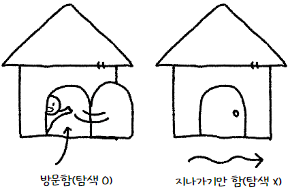
1) 전위 순회 (Preorder)
현재 노드를 부모 노드로 생각했을 때, 부모 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드 순서로 방문한다.
전위 순회는 거치는 노드를 바로 방문(출력)하기 때문에, 직관적으로 이해하기 쉽다.
전위 순회는 트리를 복사할 때 많이 사용한다.
2) 중위 순회 (Inorder)
현재 노드를 부모 노드로 생각했을 때, 왼쪽 자식 노드 -> 부모 노드 -> 오른쪽 자식 노드 순서로 방문한다.
중위 순회는 거쳐가는 노드(현재 노드)를 거쳐가기만 할 뿐, "방문"하지 않는다.
중위 순회는 이진 탐색 트리에서 정렬된 순서대로 값을 가져올 때 사용된다.
3) 후위 순회 (Postorder)
현재 노드를 부모 노드로 생각했을 때, 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 부모 노드 순서로 방문한다.
자식 노드부터 방문하는 특성이 있는 후위 순회는 트리 삭제에 많이 사용한다.
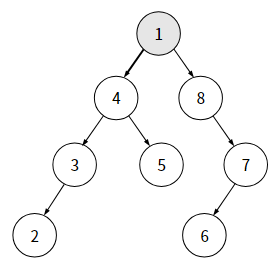
전위 순회 : 1 -> 4 -> 3 -> 2 -> 5 -> 8 -> 7 -> 6
중위 순회 : 2 -> 3 -> 4 -> 5 -> 1 -> 8 -> 6 -> 7
후위 순회 : 2 -> 3 -> 5 -> 4 -> 6 -> 7 -> 8 -> 1
12-2. 이진 트리 포인터로 표현하기
포인터로 트리를 표현하려면, 노드부터 정의해야 한다.
아래 그림처럼 노드는 "노드의 값", "왼쪽 자식 노드", "오른쪽 자식 노드"를 가진다.
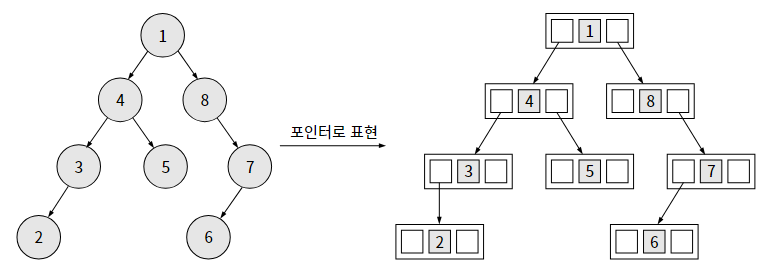
포인터로 표현한 트리는 배열과 달리 인덱스 연산을 하지 않으므로, 메모리 공간을 낭비하지 않는다는 장점이 있다.
하지만 실제 노드를 따라가도록 구현해야 하므로, 구현 난이도는 배열로 표현한 트리에 비해 높다.
13. 이진 트리 탐색하기
이진 트리에서 가장 중요한 것은, 탐색을 효율적으로 할 수 있도록 트리를 구축하는 것이다.
이진 탐색 트리 (Binary search tree)를 만들고, 이를 활용해 원하는 노드를 효율적으로 찾는 방법을 알아보자.
13-1. 이진 탐색 트리 구축하기
데이터가 3 -> 4 -> 2 -> 8 -> 9 -> 7 -> 1 순서로 들어온다고 생각하자.
이진 탐색 트리는 데이터 크기를 따져 크기가 작으면 왼쪽 자식 위치에, 크거나 같으면 오른쪽 자식 위치에 배치하는 정렬 방식을 갖고 있다. 즉, 삽입과 동시에 정렬을 하는 셈이다.

13-2. 이진 탐색 트리 탐색하기
1) 찾으려는 값이 현재 노드의 값과 같으면 탐색을 종료하고, 크면 오른쪽 노드를 탐색한다.
2) 찾으려는 값이 현재 노드의 값보다 작으면, 왼쪽 노드를 탐색한다.
3) 모든 노드를 탐색했는데 값이 없다면, 현재 트리에 찾으려는 값이 없는 것이다.
13-3. 이진 탐색 트리는 크면 오른쪽, 작으면 왼쪽
모든 탐색 알고리즘에서 탐색 효율을 개선하는 방법은 같다. 탐색 대상이 아닌 노드를 한 번에 많이 제외하면 된다!
이진 탐색 트리의 구축 방식 자체가 갖는 특성은, 데이터 크기에 따라 하위 데이터 중 한 방향을 검색 대상에서 제외하므로 검색이 빨라지는 것이다.
13-4. 이진 탐색 트리의 시간 복잡도
이진 탐색 트리의 시간 복잡도는 "트리 균형"에 의존한다.
트리 균형 : 각 노드의 차수(degree)가 비슷하게 유지 되면서, 각 노드의 자식 노드 수가 비슷하게 유지될 때
또는 왼쪽과 오른쪽 서브 트리의 높이 차가 1 이하인 경우, 그렇지 않으면 치우친 이진 트리 (Degenerate binary tree)
저장된 노드가 N개인 균형 이진 탐색 트리 (Balanced binary search tree)의
삽입, 탐색 연산의 시간 복잡도는 -> O(logN)이다.
균형 이진 탐색 트리는 또 세부적으로 AVL 트리, 레드-블랙 트리 등으로 구분하여 부른다.
균형 이진 탐색 트리는 탐색 연산 횟수가 트리 높이 logN에 비례하므로, 탐색 시간 복잡도를 O(logN)으로 유지할 수 있다.
※ 다만 균형 이진 탐색 트리 구현은 난이도가 너무 높아서 코딩 테스트에는 나오지 않을 가능성이 매우 높다고 한다.
14. 너비 우선 탐색 (BFS)는 왜 항상 최단 경로를 보장할까?
너비 우선 탐색은 현재 지점에서 갈 수 있는 모든 경로로 뻗어나가는 방식이다.
반면 깊이 우선 탐색(DFS)은 모든 경로 중 한 방향의 경로만 선택해서, 끝까지 뻗어나가는 방식이다.
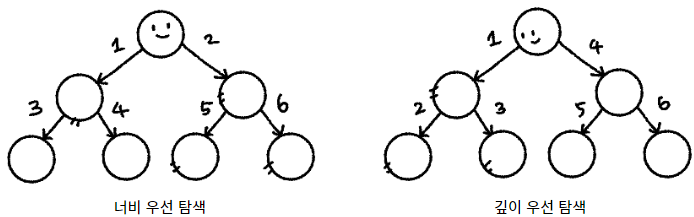
미로에서도 마찬가지이다. BFS는 각 지점에서 갈 수 있는 모든 방향으로 뻗어나가기 때문에,
각 지점의 단계별 탐색 길이가 같으므로, 도착 지점까지의 최단 거리를 찾을 수 있다.
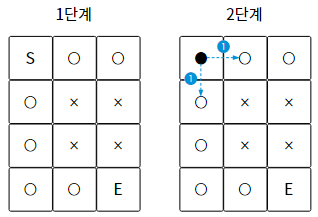
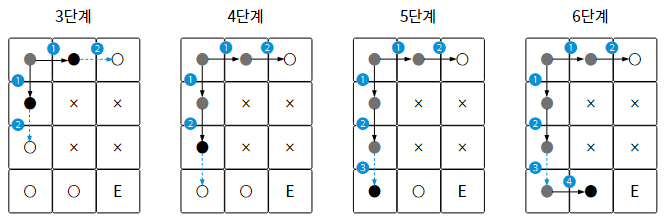
또한 너비 우선 탐색은 각 과정마다 최선의 탐색을 하므로 이미 거쳐온 경로는 다시 탐색하지 않아도 된다.
보통 visited라는 리스트를 구현해서 지나온 경로인지 판단한다.
15. 집합 (Set)
집합은 순서와 중복이 없는 원소들을 갖는 자료구조이다.
집합은 특성에 따라 부르는 말이 다양하다. 여러 종류의 집합이 있지만,"상호배타적 집합"에 집중해보자.
상호배타적 집합 : 교집합이 없는 집합 관계

A = {1, 2, 3}이고, B = {4, 5, 6, 7}이므로 이들을 상호배타적 집합이라고 한다.
15-1. 상호배타적 집합의 특성을 활용하는 분야
코딩 테스트에서 상호배타적 집합은 "그래프 알고리즘"에서
많이 활용하기 때문에 중요하다!
그래프 알고리즘에서는 흔히 사이클을 확인하는데, 그 작업에 상호배타적 집합 개념을 활용한다.
이 외에도 상호배타적 집합 개념을 활용하는 분야는 다양하다.
1) 이미지 분할 : 이미지를 서로 다른 부분으로 나누는 데 사용한다.
EX) 사람과 배경을 겹치지 않게 분할하는 데 사용될 수 있다.
2) 도로 네트워크 구성 : 도로를 구축할 때, 각 도로를 서로 교차하지 않도록 설계하는 데 사용한다. -> 교차로의 혼잡이 줄어든다.
3) 최소 신장 트리 알고리즘 구현 : 또는 간선을 추가할 때마다 사이클을 형성하는지 체크할 때도 사용한다.
4) 게임 개발 : 캐릭터의 동작을 자연스럽게 구현할 수 있다.
EX) 플레이어와 적 캐릭터가 충돌할 때, 이 두 캐릭터가 겹치지 않도록 하는 데 사용한다.
5) 클러스터링 작업 : 여러 작업이 서로 겹치지 않도록 구성할 수 있다.
이렇게 작업 간의 의존관계가 없으면 동시에 여러 작업을 진행할 수 있다는 장점이 있다.
16. 집합의 연산
보통 집합은 배열을 활용한 트리로 구현한다! 그리고 각 집합에는 대표 원소가 있어야 한다.
대표 원소 : 집합의 원소 중 집합을 대표하는 역할을 한다.
다만 지금은 집합의 형태를 트리로 표현할 것이므로, 이후에는 대표 원소를 "루트 노드"라고 부르자.
※ 개념적으로 집합의 대표 원소와 트리의 루트 노드는 같다.
16-1. 배열로 집합을 표현하는 것이란?
집합을 배열로 표현한다는 것은 하나의 배열로 상호배타적 관계를 가지는 집합을 모두 표현한다는 것이다.
그리고 집합을 트리 형태로 표현할 때는 이것을 기억하자!
배열의 인덱스는 자신을, 배열의 값은 부모 노드를 의미한다.
EX) disjoint_set[9] = 3 이라면 -> 9번 노드의 부모노드는 3 이라는 것이다.
그러면 루트 노드는 부모가 없으므로(= 부모 노드가 자기 자신이므로) 배열의 값 자체가 배열의 인덱스와 동일하다!

그렇다면 집합을 표현하는 데 사용하는 배열의 크기는 어때야 할까?
-> 배열의 인덱스가 모든 집합의 원소를 표현할 수 있으면 된다. EX) 가장 큰 원소가 9이므로, 배열의 크기는 10
16-2. 집합 표현 완벽 정리하기
그럼 다른 그림을 보면서 집합 개념을 완벽히 정리해보자.
위와 같은 집합을, disjoint_set 배열을 활용한 트리로 나타내면 다음 특성을 가지게 된다.
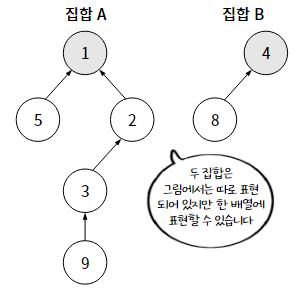
1. 각 집합 A, B의 루트 노드는 1과 4이다. 즉, disjoint_set[1] = 1, disjoint_set[4] = 4이다. (인덱스와 값이 같다)
2. disjoint_set[3] = 2, disjoint_set[2] = 1을 해석해보면, 집합 A의 원소 3의 부모는 2, 원소 2의 부모는 1이라는 뜻이다.
그러면 결국 '원소 3은 원소 1이 루트 노드인 집합에 속한다'라고 이야기할 수 있다.
3. 집합 A, 집합 B를 표현할 배열의 크기를 10으로 한다.
4. 두 집합은 하나의 배열(disjoint_set)로 표현할 수 있다!
※ 집합의 개수는 루트 노드의 개수를 보면 된다. -> 즉, 배열의 인덱스와 값이 같은 횟수를 세면 된다!
16-3. 집합을 배열로 구현하기
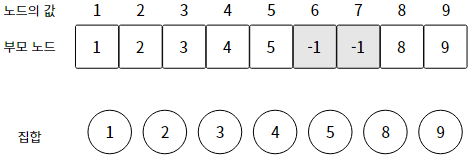
17. 유니온-파인드 알고리즘 (Union & Find)
집합에 주로 쓰이는 연산은 합치기(Union)와 탐색(Find)이다.
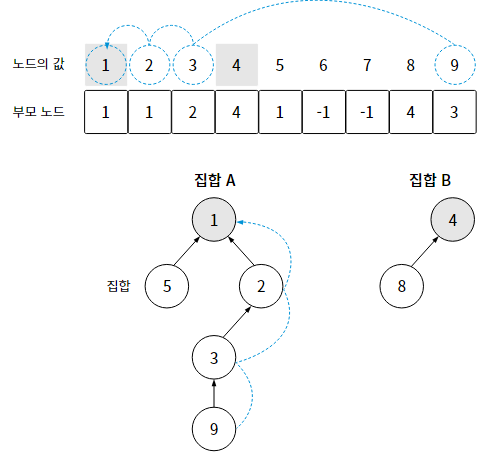
17-1. 파인드 (Find) 연산
특정 노드의 루트 노드가 무엇인지 탐색하는 방법이다.
보통 파인드 연산은 특정 노드가 같은 집합에 있는지 확인할 때 사용한다.
1) 현재 노드의 부모 노드를 확인한다. 부모 노드를 확인하다가, 루트 노드이면 파인드 연산을 종료한다.
2) 1번 단계에서 파인드 연산이 종료되지 않았다면 -> 1번을 반복한다.
이와 같은 탐색 연산은 "재귀 함수"로 구현한다. 구현은 간단하지만, 최악의 경우 시간 복잡도가 O(N)일 수 있다.
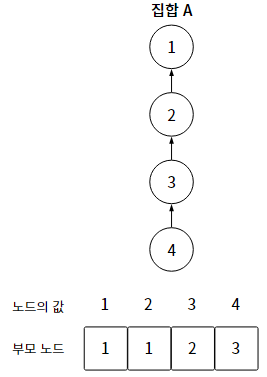
이런 단점을 개선하기 위해 "경로 압축"을 활용할 수 있다!
경로 압축 : 집합 형태를 유지하면서도 트리 높이를 줄이는 것
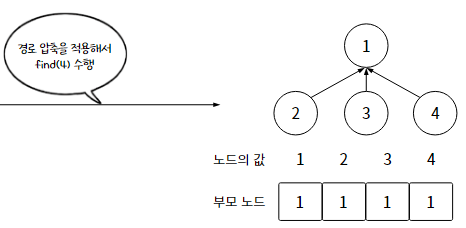
경로 압축 전후의 트리를 비교하면, 트리 깊이가 낮아지기 때문에 -> 파인드 연산 횟수가 줄어든다!
※ 경로 압축은 집합을 구성하는 트리를 평평하게(flatten) 만들어서, 파인드 연산을 효율적으로 할 수 있게 한다.
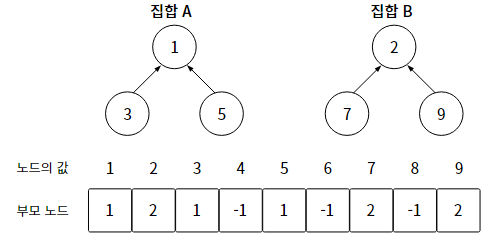
17-2. 합치기(Union) 연산
두 집합을 하나로 합치는 연산이다. -> 즉, 두 집합의 루트 노드를 같게 하는 것이다.
이때 루트 노드는 원래 두 집합의 루트 노드 중 하나가 하면 된다.
1) 두 집합에 파인드 연산을 통해 루트 노드를 찾는다.
2) 찾은 두 루트 노드의 값을 비교한다.
3) 두 집합의 루트 노드를 같게 함으로써, 두 집합을 합친다.
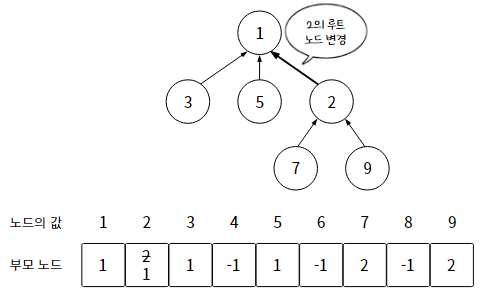
17-3. 합치기 연산 비용 문제, 랭크(Rank)로 해결하자
합치기 연산은 트리의 깊이가 깊어질수록 연산 비용이 커진다는 단점이 있다. 이를 개선하기 위해서 랭크라는 개념을 쓴다.
랭크 (Rank) : 현재 노드를 기준으로 하였을 때, 가장 깊은 노드까지의 경로 길이
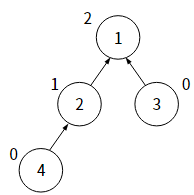
랭크 기반으로 합치기 (Union) 연산하기
1) 두 노드의 루트 노드를 구한다.
2) 1에서 구한 루트 노드의 랭크를 비교한다.
2-1) 랭크값이 다르면, 랭크값이 큰 루트 노드를 기준으로 삼는다.
즉, 랭크가 더 큰 루트 노드를 랭크가 작은 루트 노드의 부모 노드로 바꾼다. (이때 트리는 더 깊어지지 않으므로 랭크값도 변하지 않는다!)
2-2) 랭크값이 값으면, 루트 노드를 아무거나 선택해서 합치고, 최종 루트 노드의 랭크에 1을 더한다.

18. 그래프 (Graph)
그래프는 노드(Vertex)와 간선(Edge)을 이용한 비선형 데이터 구조이다. 보통 그래프는 데이터 간의 관계를 표현한다.
데이터 -> 노드로, 데이터 간의 관계나 흐름 -> 간선으로 표현한다. 간선은 방향이 있기도 하고, 없기도 하다.
만약 관계나 흐름에서 정도를 표현해야 한다면 가중치(Weight)라는 개념을 추가한다.
18-1. 그래프의 특징과 종류
그래프는 방향성, 가중치, 순환 특성에 따라 종류를 구분할 수 있다.
1) 방향성 : 흐름을 표현한다
방향이 있는 간선을 포함하면 방향 그래프 (Directed graph),
방향이 없는 간선을 포함하면 무방향 그래프 (Undirected graph) 라고 한다.
2) 가중치 : 흐름의 정도
어떤 데이터는 흐름의 방향뿐 아니라, 흐름의 정도도 간선에 표현하고자 한다.
가중치가 있는 그래프를 가중치 그래프 (Weight graph) 라고 한다.
3) 순환 : 시작과 끝의 연결 여부를 확인
특정 노드에서 시작해서, 간선을 따라 다시 돌아오는 경로가 있는 것을 말한다.
순환이 존재하는 그래프는 순환 그래프 (Cycle graph),
순환이 존재하지 않는 그래프는 비순환 그래프 (Acyclic graph) 라고 한다.
18-2. 그래프 구현 방식 2가지
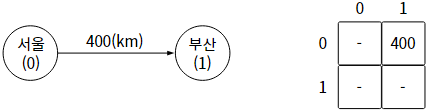
1. 인접 행렬(Adjacency matrix)로 그래프 구현하기
인접 행렬은 보통 "배열"을 활용하여 구현한다.
배열의 인덱스 = 노드, 배열의 값 = 간선의 가중치, 인덱스의 세로 방향 = 출발 노드, 인덱스의 가로 방향 = 도착 노드
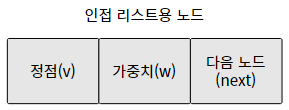
2. 인접 리스트(Adjacency list)로 그래프 구현하기
먼저 다음과 같이 값(v), 가중치(w), 다음 노드(next)를 적절하게 묶은 노드를 정의한다.
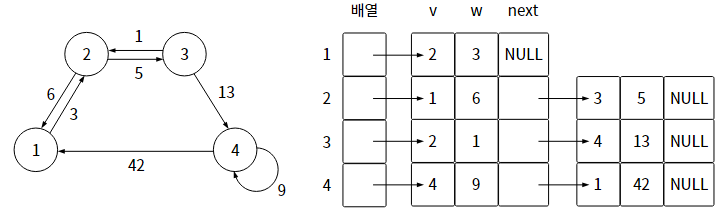
그리고 아래 2단계로 동작한다.
1) 노드 개수만큼 배열을 준비한다.
2) 배열의 인덱스는 각 시작 노드를 의미하며, 배열의 값에는 다음 노드를 연결한다.
18-3. 인접 행렬과 인접 리스트의 장단점
1. 인접 행렬의 장단점
단점 1) 인접 행렬로 희소 그래프 (Sparse graph)를 표현할 때, 공간 낭비가 심하다.
인접 행렬은 크기가 고정되어 있고, 최악의 경우를 고려해서 노드가 N개 있으면, N x N 크기의 인접 행렬이 필요하다.
그런데 희소 그래프는 간선 개수가 적으므로 N x N 크기의 인접 행렬 중 대부분은 사용하지 않게 된다.
단점 2 ) 노드들의 값의 차이가 매우 큰 그래프를 표현할 때도, 공간 낭비가 심하다.
EX) 1, 2, 3, 999... 와 같은 노드들이 있다면 가장 큰 노드의 값인 999를 기준으로 인접 행렬의 크기를 잡게 된다.
장점 1) 간선의 정보를 확인할 때, 시간 복잡도가 O(1) 이다.
EX) 노드 2에서 노드 93이 연결되어 있는 지 확인하고 싶다면, array[2][93]을 확인하면 된다.
장점 2) 구현 난이도가 낮다!
2. 인접 리스트의 장단점
인접 리스트는 인접 행렬과 정반대의 장단점을 가진다.
장점 1) 실제 연결된 노드에 대해서만 노드의 값을 배열에 담아 연결한다. 그래서 "보통은" 메모리 사용이 적다.
※ 모든 노드마다 간선이 연결되어 있을 때는 비효율적이지만, 그런 경우는 굉장히 드물다.
단점 1) 간선 정보를 확인할 때, 시간 복잡도가 O(N) 이다.

보통은 시간 복잡도에서 이점이 있는 "인접 행렬" 방식으로 그래프 문제를 푼다.
특히 문제에서 노드 개수가 1,000개 미만으로 주어진다면 -> 인접 행렬을 사용하자.
※ 노드의 데이터가 숫자가 아니라 문자열이면, 문자열을 숫자로 매핑하여 인접 행렬의 인덱스로 사용하면 된다.
19. 그래프 탐색
그래프 탐색 방법에는 크게 DFS(깊이 우선 탐색), BFS(너비 우선 탐색) 2가지가 있다.
1. 깊이 우선 탐색 (Depth-First Search)
시작 노드부터 탐색을 시작해서, 최대 깊이 노드까지 이동하며 차례대로 방문한다.
그러다가 탐색할 노드가 없다면, 최근에 방문했던 노드로 되돌아간 다음, 가지 않은 노드를 방문한다.
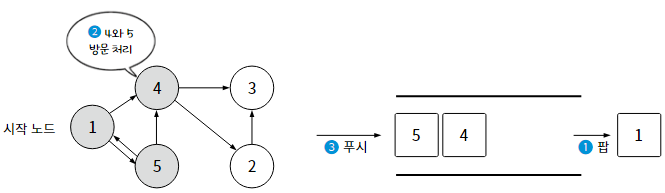
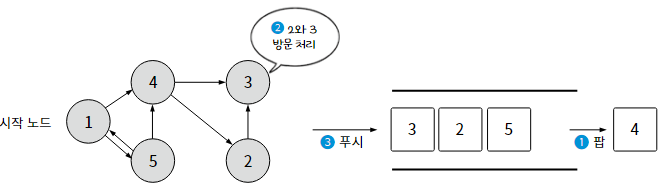
탐색을 하려면 일단 시작 노드를 정하고, 스택에 시작 노드를 푸시한다.
스택에 있는 노드는 아직 방문하지 않았고, 방문 예정인 노드이다. 그 다음, 아래 4단계를 반복한다.
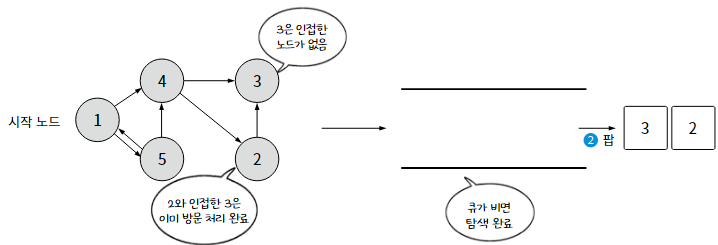
1) 스택이 비었는지 확인한다. 스택이 비어있다면, 방문할 수 있는 모든 노드를 방문했다는 의미이므로 탐색을 종료.
2) 스택에서 노드를 팝한다. 팝한 원소는 최근에 스택에 푸시한 노드이다.
3) 팝한 노드의 방문 여부를 확인한다. 아직 방문하지 않았다면, 그 노드를 방문 처리한다.
4) 방문한 노드와 인접한 모든 노드를 확인한다. 그리고 그 중에서 아직 방문하지 않은 노드를 스택에 푸시한다.
스택은 FILO(선입후출) 구조이므로, 방문 순서를 오름차순으로 고려한다면 역순으로 노드를 푸시해야 한다.
이 4가지 단계를 구현할 때, 다음 3가지 사항을 고려해야 한다.
고려 1) 탐색할 노드가 없을 때까지, 간선을 타고 내려갈 수 있어야 한다.
고려 2) 가장 최근에 방문한 노드를 알아야 한다.
고려 3) 이미 방문한 노드인지 확인할 수 있어야 한다.
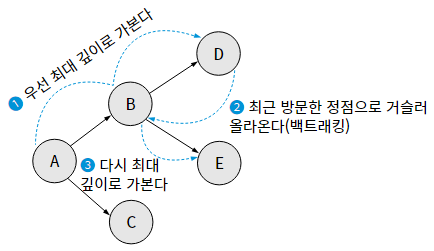
탐색하고 있는 방향의 역방향으로 되돌아가는 동작을 백트래킹(Back tracking)이라고 한다.
스택은 최근에 푸시한 노드를 팝할 수 있으므로 최근 방문 노드를 팝 연산으로 쉽게 확인 할 수 있다.
1-1. 스택을 활용한 깊이 우선 탐색
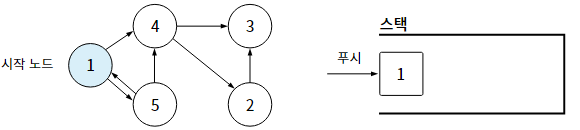


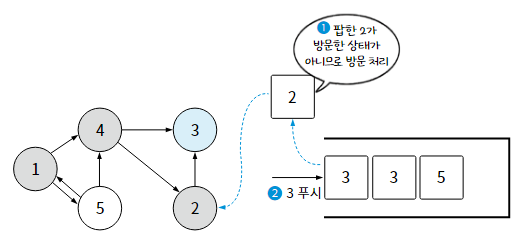

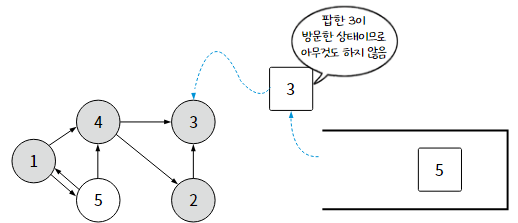
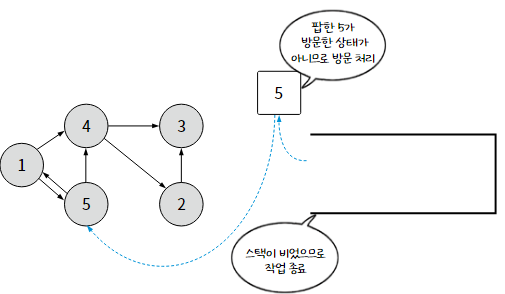
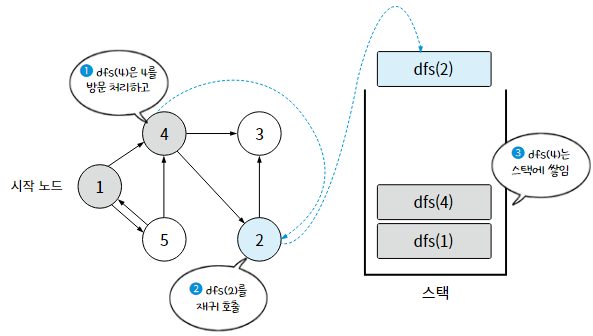
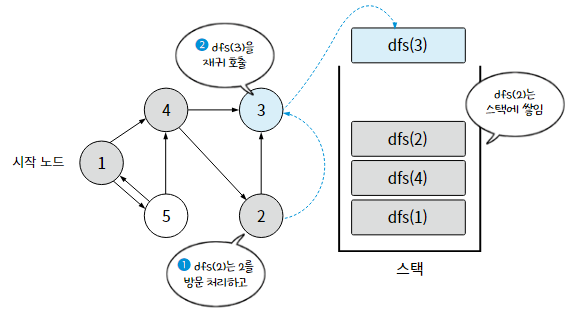
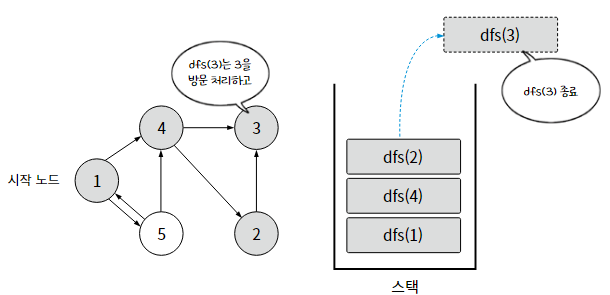
1-2. 재귀 함수를 활용한 깊이 우선 탐색
재귀 함수를 호출할 때마다, 호출된 함수는 시스템 스택이라는 곳에 쌓이므로 DFS에 활용할 수 있다.
dfs(N) : N번 노드를 방문 처리하고, N번 노드와 인접한 노드 중 아직 방문하지 않은 노드를 탐색



2. 너비 우선 탐색 (Breadth-First Search)
시작 노드와 거리(간선 가중치 X)가 가장 가까운 노드를 우선하여 방문하는 알고리즘이다.
거리 : 시작 노드와 목표 노드까지의 차수(degree)
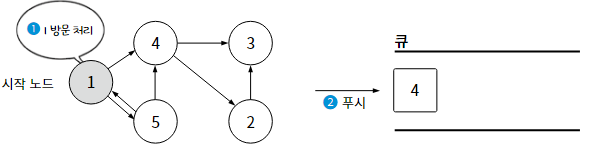
가장 먼저 시작 노드를 큐(Queue)에 푸시하면서 방문 처리를 한다. 그리고 아래 3단계를 반복한다.
1) 큐가 비었는지 확인한다. 큐가 비었다면, 방문할 수 있는 모든 노드를 방문했다는 의미이다. (탐색종료)
2) 큐에서 노드를 팝한다.
3) 팝한 노드와 인접한 모든 노드를 확인하고, 그 중 아직 방문하지 않은 노드를 큐에 푸시하며 방문 처리한다.
이 과정을 코드로 구현할 때, 다음 2가지 사항을 고려해야 한다.
고려 1) 현재 방문한 노드와 직접 연결된 모든 노드를 방문할 수 있어야 한다.
고려 2) 이미 방문한 노드인지 확인할 수 있어야 한다.
2-1. 큐를 활용한 너비 우선 탐색

19-3. DFS와 BFS 비교
1. 깊이 우선 탐색 : 깊이 탐색 후, 되돌아오는 (= 백트래킹)
모든 가능한 해를 찾는 백트래킹 알고리즘을 구현할 때나, 그래프의 사이클을 감지해야 하는 경우 활용한다.
코딩 테스트에서는 최단 경로를 찾는 문제가 아니라면, 깊이 우선 탐색을 우선 고려해보는 것이 좋다!
2. 너비 우선 탐색 : 최단 경로를 보장한다
시작 노드로부터 직접 간선으로 연결된 모든 노드를 먼저 방문하기 때문에, 찾은 노드가 시작 노드로부터 최단 경로임을 "보장"한다.
미로 찾기 문제에서 최단 경로를 찾거나, 네트워크 분석 문제를 풀 때 활용한다.
※ 방문 처리 시점이 다른 이유
깊이 우선 탐색은 스택에 "다음에 방문할 인접한 노드를 푸시"한다.
즉, 스택에 푸시할 노드는 방문 예정인 노드이므로, 팝하면서 방문 처리를 한다.
반면 너비 우선 탐색은 큐에 "지금 방문할 노드를 푸시"한다. 그래야 인접한 노드부터 먼저 탐색할 수 있다.
20. 그래프 최단 경로 (Shortest path) 구하기
가중치가 없는 그래프에서는 간선 개수가 가장 적은 경로가 최단 경로이다.
가중치가 있는 그래프에서는 이동할 때 거치는 간선 가중치의 총합이 최소가 되는 경로를 최단 경로라고 한다.
1. 다익스트라 (Dijkstra) 알고리즘
가중치가 있는 그래프의 최단 경로를 구하는 문제는 대부분 다익스트라 알고리즘을 사용한다!
1단계) 시작 노드를 설정하고, 시작 노드로부터 특정 노드까지의 최소 비용을 저장할 공간과 직전 노드를 저장할 공간을 마련한다.
1-1) 최소 비용을 저장할 공간은 INF로 초기화 한다.
1-2) 시작 노드의 최소 비용은 0, 직전 노드는 자기자신으로 한다.
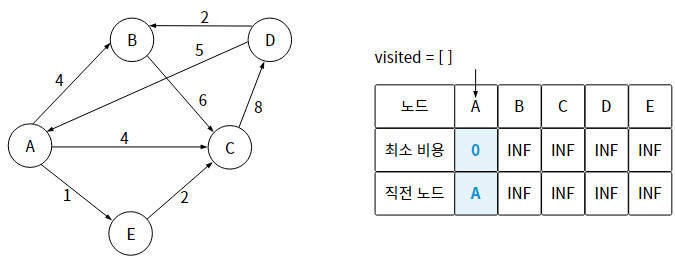
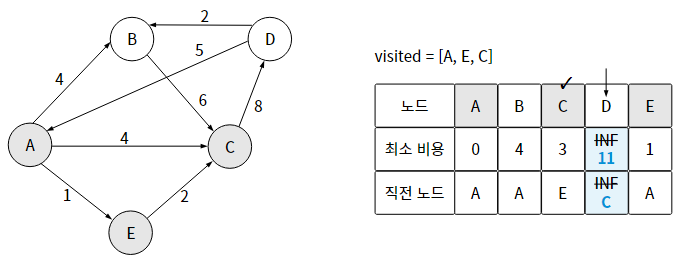
2단계) 해당 노드를 통해 방문할 수 있는 노드 중 (= 아직 방문하지 않은 노드 중)에서 현재까지 최소 비용이 가장 적은 노드를 선택한다.
2-1) 해당 노드를 거쳐서 각 노드까지 가는 최소 비용과 이전 최소 비용과 비교하여, 더 작은 값으로 갱신한다.
2-2) 이때 직전 노드도 같이 갱신한다.
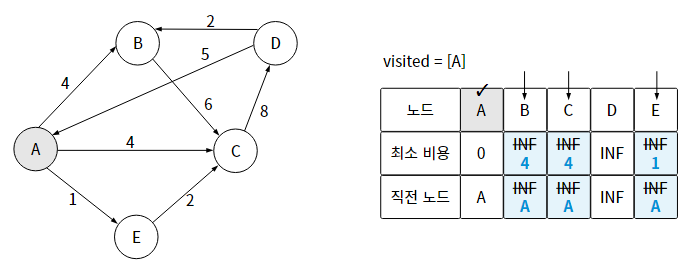

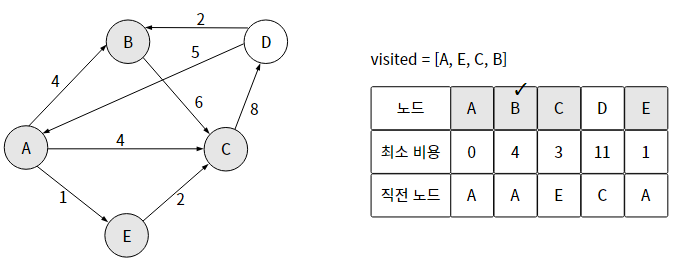
3단계) 노드 개수에서 1을 뺀 만큼 반복한다. (N-1)
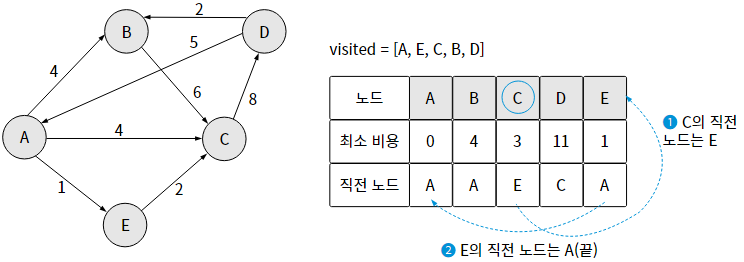
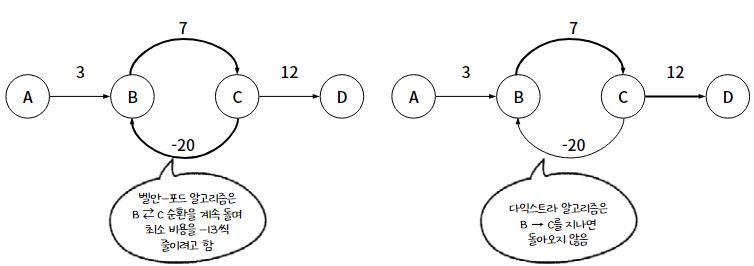
※ 다익스트라 알고리즘은 음의 가중치가 있는 그래프에서는 제대로 동작하지 않는다.
다익스트라 알고리즘은 그리디 알고리즘과 원리가 같기 때문에 한 번 방문한 노드는 다시 고려하지 않기 때문이다
그럼에도 다익스트라 알고리즘은 성능이 매우 뛰어나고, 대부분 음의 가중치를 가지지 않으므로 많이 사용한다!
2. 벨만-포드 (Bellman-ford) 알고리즘
벨만-포드 알고리즘은 매 단계마다 모든 간선의 가중치를 다시 확인하여, 최소 비용을 갱신한다.
따라서 음의 가중치를 가지는 그래프에서도 최단 경로를 구할 수 있다.
1단계) 시작 노드의 최소 비용은 0, 나머지 노드는 INF로 초기화한다. 이후 최소 비용을 갱신할 때, 직전 노드도 갱신한다.
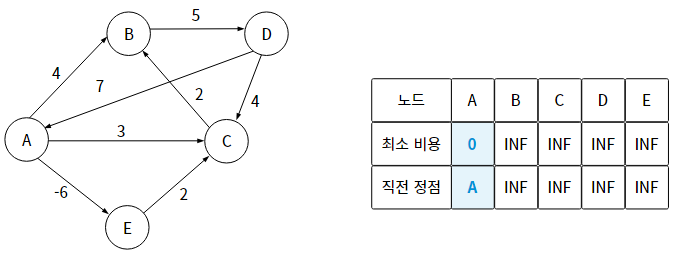
2단계) 이 연산들을 "노드 개수 - 1"번 반복한다.
2-1) 시작 노드에서 갈 수 있는 각 노드에 대하여,
전체 노드 각각을 거쳐갈 때 현재까지 최소 비용보다 더 적은 최소 비용이 있다면 갱신한다.
2-2) 최소 비용을 갱신할 때, 그 노드의 직전 정점 값도 같이 갱신한다.
3단계) 2단계를 마지막으로 한번 더 수행하여, 갱신되는 최소 비용이 있는지 확인한다.
만약 있다면, 음의 순환이 있다는 것을 의미한다!

노드 A에서 B를 거쳐 각 노드까지 가는 최소 비용도 갱신해보자.


노드 A에서 D를 거쳐가는 방법은 없으므로, 갱신하지 않는다.
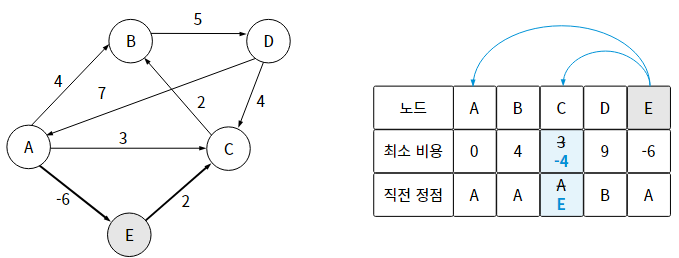
여기까지가 첫 번째 반복이었다. 위에서 했던 과정을 이렇게 '노드 개수 - 1'번 반복하면 된다.
Q. 왜 벨만-포드 알고리즘은 '정점 개수 - 1'만큼 반복할까?
A. 매 반복마다 최단 경로가 1개씩 확정되므로!
벨만-포드 알고리즘이 연산을 K번 반복하면 K개의 간선에 대한 최단 경로를 구할 수 있다.

Q. 벨만-포드 알고리즘에서 왜 한 번 더 연산을 반복할까?
A. 음의 순환을 찾기 위해
흔히 벨만-포드 알고리즘의 한계점으로 '음의 순환이 있을 때, 최단 경로를 구하지 못한다'를 자주 말한다.
그러나 엄밀히 말하자면, 그래프에 음의 순환이 있다면 어떤 알고리즘도 최단 경로를 구할 수 없다!
다만, 음의 가중치를 다루는 최단 경로 알고리즘은 음의 순환에 빠질 수 있다는 것이다.
다익스트라 알고리즘은 음의 가중치가 있는 그래프에서 동작하지 못하므로, 아예 언급도 안되는 것이다.
즉, 오히려 벨만-포드 알고리즘의 특징을 "음의 순환을 감지할 수 있는 것"으로 봐야 한다.

21. 백트래킹 (Backtracking)
이전에 배운 DFS, BFS는 모든 경우의 수를 탐색하는 완전 탐색이었다.
완전탐색은 거의 답을 찾을 수 있지만, 대부분의 경우에서는 비효율적이다.
가능성이 없는 곳에서는 더 이상 탐색하지 않고 되돌아가고,
가능성이 있는 곳만 탐색하는 알고리즘을 백트래킹 알고리즘이라고 한다.
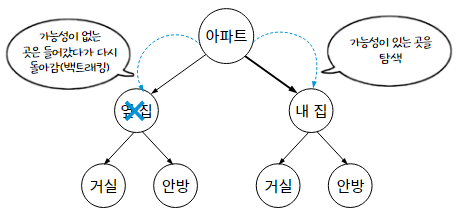
백트래킹 알고리즘은 문제마다 효율이 달라지므로 시간 복잡도를 특정하여 정의하기 어렵다.
※ 사실 DFS도 더 이상 탐색할 경로가 없을 때 다시 돌아갔으므로, 백트래킹을 한 것이다.
그러나 주된 백트래킹 알고리즘은 해가 있을 가능성이 없을 경우를 매번 판단해서 백트래킹을 활용한다.
21-1. 유망 함수 (Promising function)
백트래킹 알고리즘의 핵심은 '해가 될 가능성을 판단하는 것'이다. 그 가능성은 유망 함수라는 것을 정의하여 판단한다.
실제 백트래킹 알고리즘도 이런 4단계로 진행된다.
1단계) 유효한 해의 집합을 정의한다.
2단계) 1단계에서 정의한 집합을 그래프로 표현한다.
3단계) 유망 함수를 정의한다.
4단계) 백트래킹 알고리즘을 활용해서 해를 찾는다.
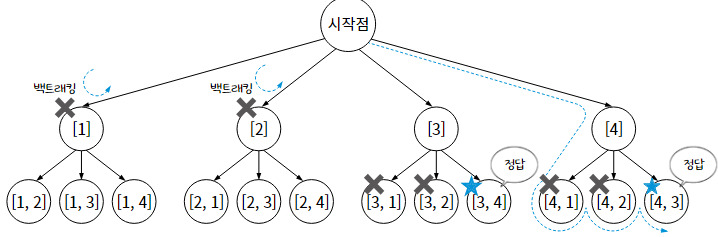
예제 Q. {1, 2, 3, 4} 중 2개의 숫자를 뽑아서 6을 초과하는 경우를 구하시오.
1단계 : 유효한 해의 집합을 정의한다. -> 여기에서는 순열로 구했다.

2단계 : 정의한 해의 집합을 그래프로 표현한다.

3단계 : 이 예제에는 "처음에 뽑은 숫자가 3 미만이면 백트래킹한다"라는 전략을 사용한다.
이렇게 특정 조건(전략)을 정의하는 것을 유망 함수를 정의한다고 하는 것이다.
4단계 : 백트래킹 알고리즘을 활용해서 해를 찾으면 된다.
21-2. 백트래킹 알고리즘을 문제에 적용하기
백트래킹으로 해결할 수 있는 대표적인 문제인 "부분 집합 합" 문제와 "N-Queen" 문제를 살펴보자.
1) 부분 집합 합 (Sum of subset)
1 ~ N까지 숫자를 조합했을 때, 합이 K가 되는 조합을 찾는 문제이다.
만약 N = 4, K = 5일 때, 완전 탐색을 한다면 이렇게 할 것이다. 시간복잡도는 O(2^N)일 것이다.

말 그대로 완전히 모든 경우의 수를 탐색하여 총 16번의 탐색을 진행했다.
백트래킹으로 풀기
조건 1 : 현재 조합으로 합이 K가 되면, 더 이상 탐색하지 않기
조건 2 : 해당 숫자를 조합하여 합이 K 이상이 되면, 더 이상 탐색하지 않기

※ 사실 유망 함수는 같은 문제에서도 다양하게 정의할 수 있다!
이 문제만 보더라도 숫자를 1부터 체크하고 마지막 숫자를 알고 있으므로,
만약 "숫자 1에서 3까지 조합에서 합이 0이었다면, 4를 볼 필요가 없다"는 것도 추가로 알 수 있다.
2) N-Queen 문제
체스의 퀸을 N x N 체스판에 N개 배치했을 때, 서로를 공격할 수 없는 위치에 놓을 수 있는 방법이 있는지 찾는다.
역시 완전 탐색으로 문제를 푼다면, N개의 퀸을 각 줄에 놓는 방법은 N개이므로 시간 복잡도는 O(N ^ N)일 것이다.
백트래킹으로 풀기
조건 1 : 각 행마다 하나씩 퀸을 추가할 때마다, 열이나 대각선 방향에 겹치는 퀸이 있다면 더 이상 탐색하지 않기
https://sweetburble.tistory.com/46
[파이썬] 9663번. N-Queen 풀이
어차피 체스판에 놓일 퀸들은 다 다른 행, 다른 열에 있어야 한다. 그리고 서로의 대각선에 위치해 있어도 안 된다. 맨 위에 행의 1번째 열부터 확인한다. 2번째 행에 되는 열(3번째 열)이 있으면,
sweetburble.tistory.com
'알고리즘과 코딩 테스트' 카테고리의 다른 글
| 내용 정리 - [이것이 코딩 테스트다 with 파이썬] (0) | 2024.02.16 |
|---|
